Sort 개념
기준에 따라 데이터를 정렬
정렬 알고리즘 개요
정렬(Sort) 이란 데이터를 특정한 기준(이를테면 오름차순이나 내림차순)에 따라서 순서대로 나열하는 것이다. 정렬 알고리즘으로 데이터를 정렬하게 되면 이진 탐색(Binary Search)도 가능하다. 이진 탐색의 전처리 정도로 생각해도 좋을 것 같다. 정렬알고리즘의 종류는 많은데, 기본 파이썬 제공 라이브러리를 활용해서 효과적인 정렬 수행 방법도 가능하다.
정렬의 종류
- 선택 정렬
- 삽입 정렬
- 퀵 정렬
- 계수 정렬
선택 정렬
가장 작은 데이터를 선택해 맨 앞에 있는 데이터와 바꾸고, 그 다음 작은 데이터를 선택해 앞에서 두 번째 데이터와 바꾸는 과정을 반복하는 원시적인 방법을 선택 정렬(Sellection Sort)이라 한다.
1
2
3
4
5
6
7
8
9
10
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(len(array)):
min_index = i # 가장 작은 원소의 인덱스
for j in range(i + 1, len(array)):
if array[min_index] > array[j]:
min_index = j
array[i], array[min_index] = array[min_index], array[i] # 스와프
print(array)
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
해당 코드에서는 스와프(Swap) 에 대해서 이해하고 있으면 쉽게 알 수 있다.
선택 정렬의 시간 복잡도
선택 정렬은 N-1 번 만큼 가장 작은 수를 찾아서 맨 앞으로 보내야 한다. N + N-1 + N-2 … + 2 번의 연산이 필요하며, 근사치로 N(N+1)/2 로 볼 수 있으며 시간복잡도는 \(O(N^2)\) 이다. 즉 정렬해야할 데이터가 100개면 10000번의 연산이 필요하다.
삽입 정렬
선택 정렬은 하나씩 비교하기 때문에 알고리즘 문제 풀이에는 속도가 느리다는 단점이 있다. 삽입 정렬(Insertion Sort)은 데이터를 하나씩 확인하여, 각 데이터를 적절한 위치에 삽입한다 는 아이디어에서 출발한다. 삽입정렬은 첫 번째 데이터는 그 자체로 정렬되어 있다 판단하고 두번째 데이터 부터 시작하여 두번째 데이터를 첫번째 데이터와 비교하여 앞에 둘지, 뒤에 둘지 결정한다.
1
2
3
4
5
6
7
8
9
10
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
for i in range(1,len(array)):
for j in range(i, 0, -1): #인덱스 i부터 1(0전)까지 -1씩 감소하며 반복하는 문법
if array[j] < array[j-1]:#한칸씩 왼쪽으로 이동
array[j] , array[j-1] = array[j-1], array[j]
else:
break
print(array)
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
삽입 정렬의 시간 복잡도
삽입 정렬은 선택 정렬과 마찬가지로 반복문이 2번 중첩되어 시간복잡도는 \(O(N^2)\) 이다. 그러나 현재 리스트의 데이터가 거의 정렬되어 있는 상태라면 최선의 경우 \(O(N)\) 의 시간 복잡도를 가진다. 따라서 거의 정렬 되어 있는 경우에 퀵 정렬 알고리즘 보다 강할 수 있고, 데이터가 정렬되 있다면 삽입 정렬을 사용하는 것이 정답일 수 있다.
퀵 정렬
퀵 정렬(Quick Sort)는 정렬 알고리즘 중에 가장 많이 사용되는 알고리즘으로 병합 알고리즘과 비슷한 속도를 갖는다. 기준 데이터를 설정하고 그 기준보다 큰 데이터와 작은 데이터의 위치를 바꾼다 라는 아이디어로 시작한다.
퀵 정렬은 기준(피벗, Pivot) 을 설정하고 다음 큰 수와 작은 수를 교환한 후 리스트를 반으로 나누는 방식으로 동작한다. 퀵 정렬을 수행하기 전에는 피벗을 어떻게 설정할 것인지 미리 명시해야 한다. 피벗을 설정하고 리스트를 분할하는 방법에 따라서 여러 가지 방식으로 퀵 정렬을 구분하는데, 가장 대표적인 분할 방식으로 호어 분할(Hoare Partition) 을 사용하겠다.
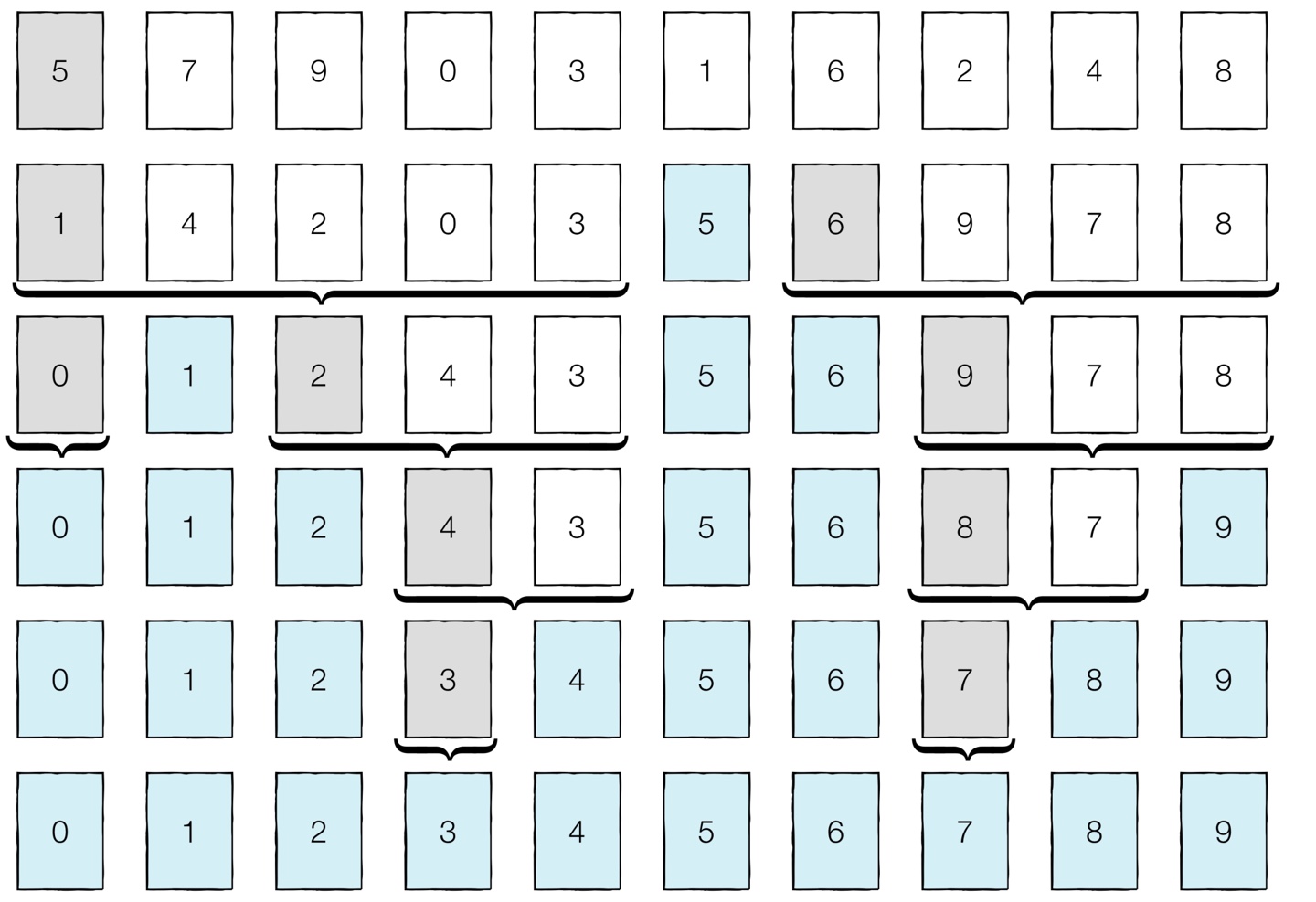
파트1 그림상 첫 번째줄의 첫 번째 데이터 5를 피벗으로 설정한다. 이후 왼쪽에서 부터 5보다 큰데이터를 선택하고, 오른쪽에서 부터 5보다 작은 데이터를 선택해 자리를 바꾼다.(7,4) 그 다음 (9,2)를 바꾼다. 그다음으로 왼쪽에서 부터 5보다 큰 수는 6이고 오른쪽에서 부터 작은 수는 1인데 이 두개는 엇갈리게 된다. 이때! 작은 데이터와 피벗의 위치를 바꾼다.(1,5) 그러면 두 번째 줄의 결과가 나온다. 번째 줄을 보게 되면 5를 기준으로 왼쪽은 모두 5보다 작고, 오른쪽은 5보다 큰 값이 나온다. 이러한 작업을 분할(Divide) 혹은 파티션(Partition)이라고 한다.
파트2 5보다 작은 왼쪽에 대해 똑같은 방식으로 실행한다.
파트3 5보다 큰 오른쪽에 대해 똑같은 방식으로 실행한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array, start, end):
if start >= end: # 원소가 1개인 경우 종료
return
pivot = start #피법은 첫 번째 원소
left = start +1
right = end
while left <= right:
# 피벗보다 큰 데이터를 찾을 때까지 반복
while left <= end and array[left]<=array[pivot]:
left += 1
# 피벗보다 작은 데이터를 찾을 때까지 반복
while right > start and array[right] >= array[pivot]:
right -= 1
# 엇갈렸다면 작은 데이터와 피벗을 교체
if left > right:
array[right], array[pivot] = array[pivot], array[right]
# 엇갈리지 않았다면 작은 데이터와 큰 데이터를 교체
else:
array[right], array[left] = array[left], array[right]\
# 분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬 수행
quick_sort(array, start, right-1)
quick_sort(array, right+1, end)
quick_sort(array, 0, len(array) -1)
print(array)
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
파이썬의 장점을 살린 퀵 정렬 코드
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
array = [5, 7, 9, 0, 3, 1, 6, 2, 4, 8]
def quick_sort(array):
# 리스트가 하나 이하의 원소만을 담고 있다면 종료
if len(array) <= 1:
return array
pivot = array[0] # 피벗은 첫 번째 원소
tail = array[1:] # 피벗을 제외한 리스트
left_side = [x for x in tail if x<=pivot] # 분할된 왼쪽 부분
right_side = [x for x in tail if x>pivot] # 분할된 오른쪽 부분
#분할 이후 왼쪽 부분과 오른쪽 부분에서 각각 정렬을 수행하고, 전체 리스트를 반환
return quick_sort(left_side) + [pivot] + quick_sort(right_side)
print(quick_sort(array))
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
퀵 정렬의 시간 복잡도
선택 정렬과 삽입 정렬의 시간 복잡도는 \(O(N^2)\) 이다. 퀵 정렬의 평균 시간 복잡도는 \(O(NlogN)\) 이다.
계수 정렬
계수 정렬(Count Sort)알고리즘은 특정한 조건에서만 사용할 수 있지만 매우 빠른 정렬 알고리즘이다. 모든 데이터가 양의 정수인 상황에서 데이터의 개수가 N, 데이터 중 최댓값이 K일 떄 계수 정렬은 최악의 경우에도 수행시간 \(O(N+K)\) 을 보장한다. 다만 데이터의 크기 범위가 제한되어 정수 형태로 표현할 수 있을 때 만 사용 가능하다. 크기 범위가 제한된다는 것은 가장 작은 데이터와 큰 데이터의 차이가 1,000,000을 넘지 않을 때를 말한다.
계수 정렬은 일반적으로 별도의 리스트를 선언하고 그 안에 정렬에 대한 정보를 담은 다음 입력된 데이터의 count를 인덱스로 추가한 후 인덱스 숫자만큼 정렬한다.
1
2
3
4
5
6
7
8
9
10
11
# 모든 원소의 값이 0보다 크거나 같다고 가정
array = [7, 5, 9, 0, 3, 1, 6, 2, 9, 1, 4, 8, 0, 5, 2]
# 모든 범위를 포함하는 리스트 선언(모든 값은 0으로 초기화
count = [0] * (max(array)+1)
for i in range(len(array)):
count[array[i]] += 1 # 각 데이터에 해당하는 인덱스의 값 증가
for i in range(len(count)): # 리스트에 기록된 정렬 정보 확인
for j in range(count[i]):
print(i, end=' ')
1
0 0 1 1 2 2 3 4 5 5 6 7 8 9 9
계수 정렬의 시간복잡도와 공간복잡도 계수 정렬의 시간 복잡도는 \(O(N+K)\)으로 데이터의 범위만 한정되어 있다면 기수 정렬(Radix Sort)과 더불어 가장 빠르다고 볼 수 있다. 그러나 때에 따라서 비효율성을 초래할 수 있다. 데이터가 0과 999,999 단 2개라면 리스트의 크기가 100만 개가 되어야 한다. 계수 정렬은 동일한 값을 가지는 데이터가 여러 개 등장할 때 적합하다. 예를 들어 100점을 맞은 학생이 여러 명인 데이터에 적합하다. 일반적인 경우는 퀵 정렬이 유리하다. 계수 정렬의 공간 복잡도는 \(O(N+K)\) 이다.
파이썬의 정렬 라이브러리
파이썬은 기본 정렬 라이브러리인 sorted()함수를 제공한다. sorted()는 퀵 정렬과 동작 방식이 비슷한 병합 정렬을 기반으로 만들어 졌는데 병합 정렬은 일반적으로 퀵 정렬보다 느리지만 최악의 경우에도 시간 복잡도 \(O(NlogN)\)을 보장한다.
1
2
3
4
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
result = sorted(array)
print(result)
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
1
2
3
4
array = [7, 5, 9, 0, 3, 1, 6, 2, 4, 8]
array.sort()
print(result)
1
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
1
2
3
4
5
6
7
array = [('바나나',2),('사과',5),('당근',3)]
def setting(data):
return data[1]
result = sorted(array, key=setting)
print(result)
1
[('바나나', 2), ('당근', 3), ('사과', 5)]
문제에서 별도의 요구가 없이 단순히 정렬해야 하는 상황이라면 기본 정렬 라이브러리를 사용하고, 데이터의 범위가 한정되어 있으면 계수 정렬을 사용하자.
- 1. 정렬 라이브러리로 풀 수 있는 문제 : 단순히 정렬 기법을 알고 있는지 물어보는 문제로 기본 정렬 라이브러리의 사용 방법을 숙지하고 있으면 어렵지 않게 풀 수 있다.
- 2. 정렬 알고리즘의 원리에 대해서 물어보는 문제 : 선택 정렬, 삽입 정렬, 퀵 정렬 등의 원리를 알고 있어야 문제를 풀 수 있다.
- 3. 더 빠른 정렬이 필요한 문제 : 퀵 정렬 기반의 정렬 기법으로는 풀 수 없으며 계수 정렬 등의 다른 정렬 알고리즘을 이용하거나 문제에서 기존에 알려진 알고리즘의 구조적인 개선을 거쳐서 풀 수 있다.

Comments