BinarySearch 개념
범위를 반씩 좁혀가는 탐색Permalink
순차 탐색Permalink
리스트 내에서 데이터를 매우 빠르게 탐색하는 이진 탐색(Binary Search)을 이해하기 전에 순차 탐색(Sequential Search)을 먼저 이해 해야한다. 순차 탐색은 리스트 안에 있는 데이터를 찾기 위해 앞에서부터 데이터를 하나씩 차례대로 확인하는 방법이다. 보통 정렬되지 않은 리스트에서 데이터를 찾을 때 사용한다. 쉽게 구현 가능하며 특정 원소가 있는지 체크할 때 count()를 활용하기도 한다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 순차 탐색 소스코드 구현
def sequential_search(n,target, array):
# 각 원소를 하나씩 확인
for i in range(n):
# 현재의 원소가 찾고자 하는 원소와 동일한 경우
if array[i] == target:
return i+1 #현재 위치 반환, 인덱스는 0부터 시작해서 +1
print("생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.")
input_data = input().split() #입력 데이터는 리스트 형태로 저장
n = int(input_data[0]) #원소의 개수
target = input_data[1] #찾는 문자열
print("앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.")
array = input().split()
#순차 탐색 수행 결과
print(sequential_search(n,target,array))
1
2
3
4
5
생성할 원소 개수를 입력한 다음 한 칸 띄고 찾을 문자열을 입력하세요.
5 jaejin
앞서 적은 원소 개수만큼 문자열을 입력하세요. 구분은 띄어쓰기 한 칸으로 합니다.
apple banana jaejin kiwi grape
3
이진 탐색 : 반으로 쪼개면서 탐색하기Permalink
이진 탐색은 배열(혹은 리스트)의 내부 데이터가 정렬되어 있어야만 사용할 수 있는 알고리즘이다. 범위를 절반씩 좁혀가며 데이터를 탐색한다. 구체적으로 시작점, 끝점, 중간점 세개의 포인트를 두고 찾으려는 데이터와 중간점을 비교해 데이터를 찾는다.
재귀 함수로 구현한 이진 탐색 소스코드 재귀 함수로 구현한 이진 탐색 코드는 O(logN)의 시간 복잡도를 갖는다. 데이터가 2개면 1번, 4개면 2번, 8개면 3번이라고 생각하면 이해하기 쉽다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
# 이진 탐색 소스코드 구현 (재귀 함수)
def binary_search(array, target, start, end):
if start > end:
return None
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
return binary_search(array, target, start, mid - 1)
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
return binary_search(array, target, mid + 1, end)
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
1
2
3
10 7
1 3 5 7 8 11 13 15 17 19
4
반복문으로 구현한 이진 탐색 소스코드
존 벤틀리의 말에 의하면 이진 탐색 코드를 작성한 프로그래머는 10% 내외로 실제 구현은 까다롭기에 꼭 외우자. 보통 탐색 범위가 2,000만을 넘어가면 접근하면 좋다. 시간 복잡도가 O(logN)으로 매우 뛰어나기 때문이다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def binary_search(array, target, start, end):
while start <= end:
mid = (start + end) // 2
# 찾은 경우 중간점 인덱스 반환
if array[mid] == target:
return mid
# 중간점의 값보다 찾고자 하는 값이 작은 경우 왼쪽 확인
elif array[mid] > target:
end = mid - 1
# 중간점의 값보다 찾고자 하는 값이 큰 경우 오른쪽 확인
else:
start = mid + 1
return None
# n(원소의 개수)과 target(찾고자 하는 값)을 입력 받기
n, target = list(map(int, input().split()))
# 전체 원소 입력 받기
array = list(map(int, input().split()))
# 이진 탐색 수행 결과 출력
result = binary_search(array, target, 0, n - 1)
if result == None:
print("원소가 존재하지 않습니다.")
else:
print(result + 1)
1
2
3
10 7
1 3 5 7 8 11 13 15 17 19
4
트리 자료구조Permalink
이진 탐색은 전제 조건이 데이터 정렬이다. 데이터베이스는 내부적으로 대용량 데이터 처리에 적합한 트리(Tree)자료구조를 이용해 데이터가 항상 정렬되어 있다. 따라서 데이터베이스에서의 탐색은 이진 탐색과는 조금 다르지만 이진 탐색과 유사한 방법을 이용해 탐색을 하기에 데이터가 많아도 탐색하는 속도가 빠르다. 트리 자료구조는 아래의 그림 모양이며 다음의 특징이 있다.
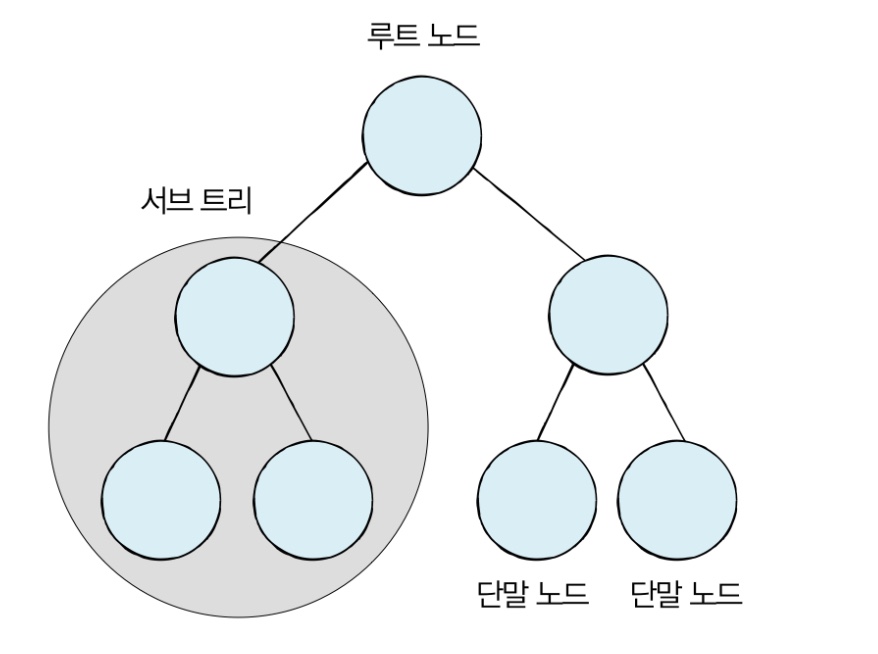
트리는 부모 노드와 지식 노드의 관계로 표현된다.
트리의 최상단 노드를 루트 노드라고 한다.
트리의 최하단 노드를 단말 노드라고 한다.
트리에서 일부를 떼어내도 트리 구조이며 이를 서브 트리라 한다.
트리는 파일 시스템과 같이 계층적이고 정렬된 데이터를 다루기에 적합하다.
이진 탐색 트리Permalink
트리 자료구조 중에서 가장 간단한 형태가 이진 탐색 트리 이다.
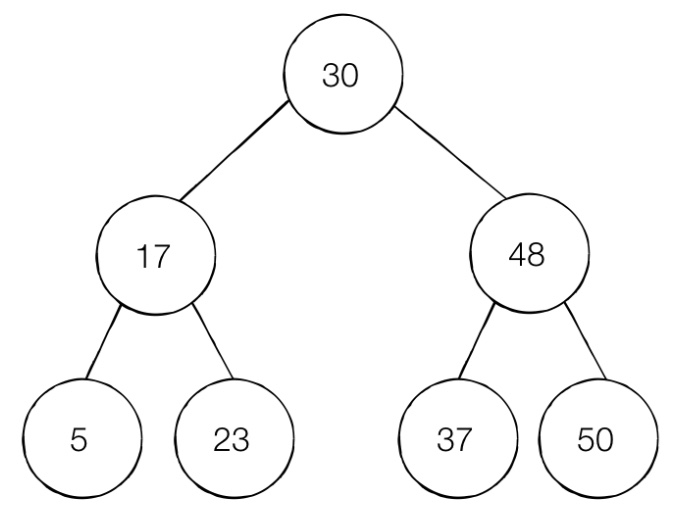
보통 이진 탐색 트리는 그림과 같으며 다음과 같은 특징을 가진다.
부모 노드보다 왼쪽 자식 노드가 작다.
부모 노드보다 오른쪽 자식 노드가 크다.
즉 왼쪽 자식 노드 < 부모 노드 < 오른쪽 자식 노드가 성립한다. 그래서 그림에서 37을 찾는다고 할때 먼저 부모 노드 30과 비교하고 부모 노드보다 크기 때문에 오른쪽을 확인한다. 오른쪽 자식 노드 48과 비교해 37이 작기 때문에왼쪽 자식 노드를 확인하여 탐색을 마친다.
빠르게 입력받기Permalink
1
2
3
4
5
import sys
#하나의 문자열 입력받기
input_data = sys.stdin.readline().rstrip()
print(input_data)
1
2
2021 03 17 jaejin choi
2021 03 17 jaejin choi
데이터의 개수가 1,000만개를 넘거나 탐색 범위의 크기가 1,000억 이상이면 이진 탐색 알고리즘을 고려하자. 이때 input() 함수를 사용하면 동작 속도가 느려 시간 초과 오답이 될 수 있으니, 입력데이터가 많을 때는 sys라이브러리의 readline()함수를 이용하면 시간 초과를 피할 수 있다. sys라이브러리를 사용할 때는 한 줄 입력하고 rstrip()함수를 꼭 호출해야 한다. 소스코드에 readline()으로 입력하면 입력 후 엔터가 줄 바꿈 기호로 입력되는데, 이 공백 문자를 제거하려면 rstrip()함수를 사용해야 한다. 코드가 짧으니 외우자.
Comments